Multiple Objectives and Tradeoffs

Lecture 27

November 20, 2023

  Activating project at `~/Teaching/BEE4750/fall2023/slides`

Review and Questions

Sensitivity Analysis

  • Sensitivity Analysis: How is uncertainty in the output(s) affected by uncertainty in the outputs?

Sensitivity Analysis: Modes

  • Factor Prioritization
  • Factor Fixing
  • Factor Mapping

Sensitivity analysis modes

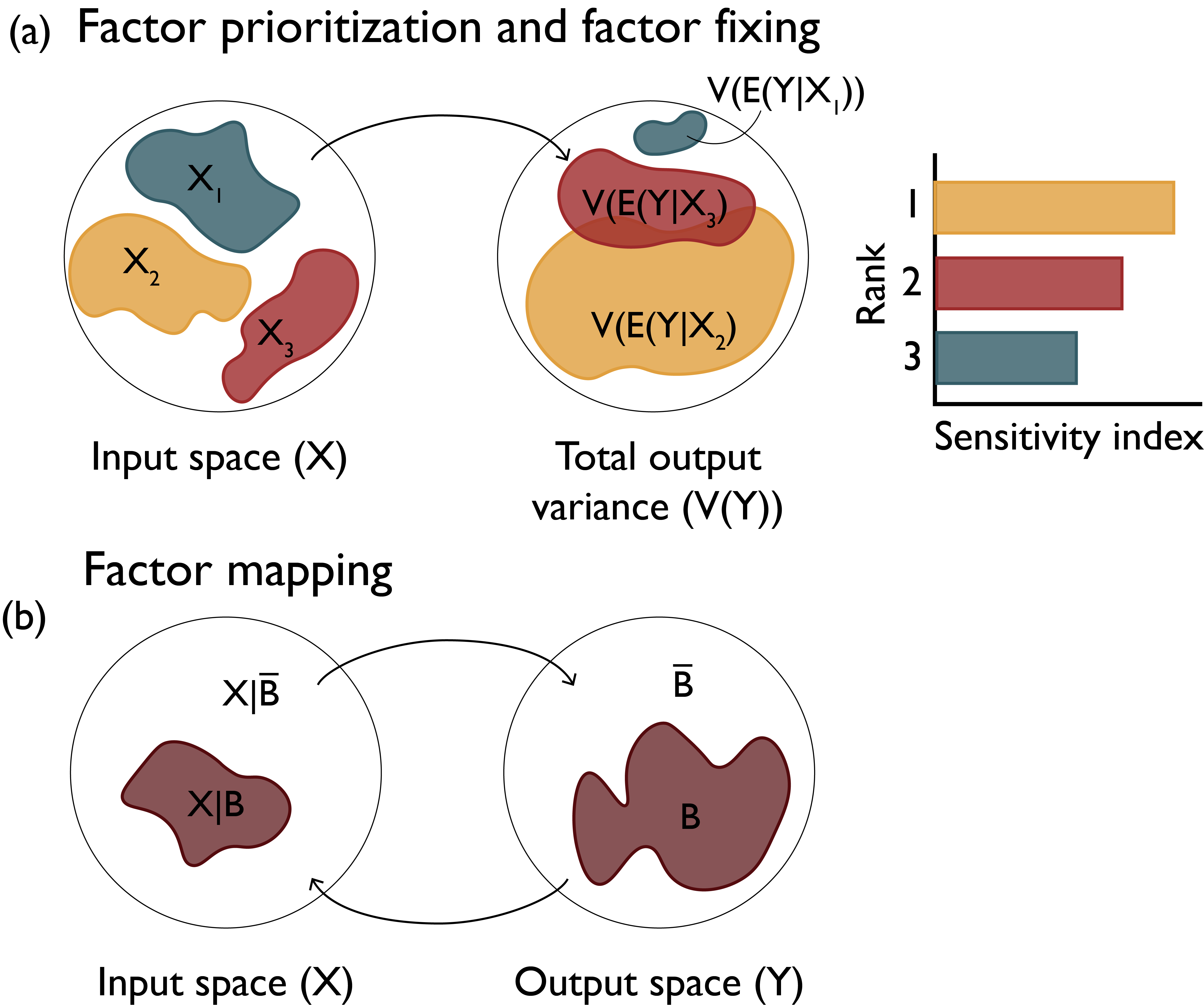
Source: Reed et al (2022)

Types of Sensitivity Analysis

  • One-At-A-Time vs. All-At-Once
  • Local vs. Global

Some Common Methods

  • Perturbation/Derivatives (OAT, Local)
  • Method of Morris (OAT, Global)
  • Sobol’ (OAT/All At Once, Global)
  • Regression: Linear Regression, Tree-based, Logistic (OAT/All At Once, Global)

Multiple Objectives

Multiple Objectives and Environmental Systems

Often have multiple objectives at play when designing or managing environmental systems:

Some examples:

  • Cost
  • Environmental quality
  • Reliability/Variability

Example: Power Systems

  • Total generation cost (including reserves);
  • CO2 emissions;
  • Resource adequacy (do we have enough resources available);
  • Reliability;
  • Other environmental impacts

Example: Reservoir Operations

  • Municipal demand;
  • Irrigation;
  • Recreation;
  • Hydropower potential;
  • Flood management;
  • Streamflow (ecosystem management)

How Can We Incorporate Multiple Objectives Into Models?

Approaches are method specific!

Key Question: what does it mean to “optimize” multiple objectives?

How Can We Incorporate Multiple Objectives Into Models?

Linear Programming:

  1. Identify thresholds and establish constraints for non-objective “objectives”;
  2. Weight objectives based on preferences, e.g. \[\min_\mathbf{x} Z(\mathbf{x}) = \sum_i w_i \hat{Z_i}(\mathbf{x}), \qquad \sum_i w_i =1\]

How Can We Incorporate Multiple Objectives Into Models?

Simulation-Optimization:

  • Could use the LP approaches
  • Can also have the simulation model (or wrapper) return multiple metrics

Back To The Key Question…

What does it mean to “optimize” multiple objectives?

Straightforward with weighting, requires but a priori elicitation of weights.

What about if we leave the objectives unaggregated?

Example: Lake Problem

Simulated 100 random decisions with two objectives:

  • Maximize mean P releases
  • Minimize probability of exceeding critical P concentration

Tradeoffs

There is a tradeoff between these two objectives:

Greater releases typically means lower reliability.

What does it mean to find an “optimum” across these two objectives?

Non-Dominated Decisions

We say that a decision \(\mathbf{x}\) is dominated if there exists another solution \(\mathbf{y}\) such that for every objective metric \(Z_i(\cdot)\), \[Z_i(\mathbf{x}) > Z_i(\mathbf{y}).\]

Non-Dominated Decisions

\(\mathbf{x}\) is non-dominated if it is not dominated by any \(\mathbf{y} \neq \mathbf{x}\).

Pareto Fronts

The set of non-dominated solutions is called the Pareto front (solutions are Pareto-optimal).

Every member of a Pareto front represents a different tradeoff between objectives.

A Priori vs A Posteriori Decision-Making

This gives us two frameworks for evaluating tradeoffs:

  1. A Priori: Establish weights ahead of time and combine objectives;
  2. A Posteriori: Identify Pareto-optimal solutions and then discuss what tradeoffs are tolerable.

Identifying Pareto Fronts

In higher dimensions, manually screening of a Pareto front is difficult.

Can use multi-objective optimization with (certain) evolutionary algorithms.

Key Takeaways

Key Takeaways

  • Management of environmental systems often involves multiple objectives.
  • Multiple objectives often have tradeoffs.
  • Can combine multiple objectives with weights (a priori decision-making) or identifying non-dominated solutions (a posteriori decision-making)
  • Set of non-dominated solutions (Pareto front) represent different choices about tradeoffs.

Course Review

Recap of Topics

Systems Dynamics and Models

  • Nonlinear dynamics result in a need to view the entire system, not individual components.
  • Models allow us to understand how a system could/would evolve under different conditions.
  • No model is “right”, results in a need to consider relevant uncertainties.

Recap of Topics

Simulating Systems:

  • Descriptive Modeling: using a model to generate data about how a system would behave
  • Typically involves looping over a domain (spatial or temporal) and evaluating
  • “Box” models

Recap of Topics

Decision-Making:

  • Prescriptive Modeling: using a model to prescribe a decision
  • Linear programming vs. simulation-optimization
  • Can stress-test decisions for robustness or with sensitivity analysis

Recap of Examples

  • Water quality
  • Air quality
  • Power systems

Key: These methods require domain knowledge but are generally applicable to all environmental systems management or design problems.

Upcoming Schedule

Upcoming Schedule

After Thanksgiving:

  • Project check-ins
  • Presentations due 12/4
  • Peer reviews, posters, evaluations/lit reviews due 12/15.