Activating project at `~/Teaching/BEE4750/fall2023/slides`
Sensitivity Analysis
Lecture 26
November 17, 2023
Review and Questions
Robustness
- Robustness: How well does your solution work under alternative model specifications/parameter choices?
- Common measures: regret, satisfycing
Sensitivity Analysis
Factor Prioritization
Many parts of a systems-analysis workflow involve potentially large numbers of modeling assumptions, or factors:
- Model parameters/structures
- Forcing scenarios/distributions
- Tuning parameters (e.g. for simulation-optimization)
Additional factors increase computational expense and analytic complexity.
Prioritizing Factors Of Interest
- How do we know which factors are most relevant to a particular analysis?
- What modeling assumptions were most responsible for output uncertainty?

Source: Saltelli et al (2019)
Sensitivity Analysis
Sensitivity analysis is…
the study of how uncertainty in the output of a model (numerical or otherwise) can be apportioned to different sources of uncertainty in the model input
— Saltelli et al (2004), Sensitivity Analysis in Practice
Why Perform Sensitivity Analysis?
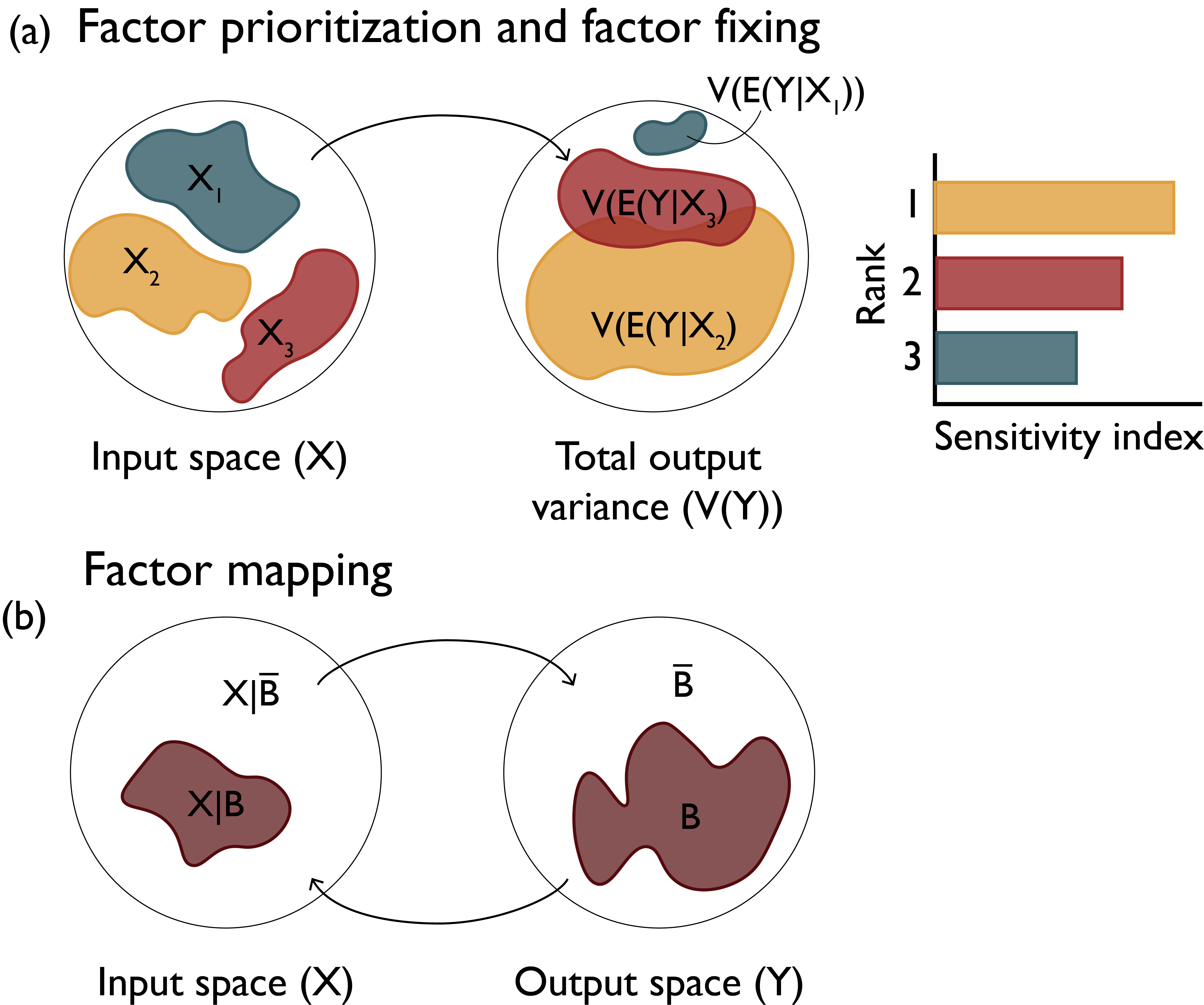
Source: Reed et al (2022)
Factor Prioritization
Which factors have the greatest impact on output variability?

Source: Reed et al (2022)
Factor Fixing
Which factors have negligible impact and can be fixed in subsequent analyses?

Source: Reed et al (2022)
Factor Mapping
Which values of factors lead to model outputs in a certain output range?

Source: Reed et al (2022)
Example: Shadow Prices Are Sensitivities!
We’ve seen one example of a quantified sensitivity before: the shadow price of an LP constraint.
The shadow price expresses the objective’s sensitivity to a unit relaxation of the constraint.
Shadow Prices As Sensitivities
Shadow Prices As Sensitivities
Sorting by Shadow Price ⇄ Factor Prioritization
Types of Sensitivity Analysis
Categories of Sensitivity Analysis
- One-at-a-Time vs. All-At-A-Time Sampling
- Local vs. Global
One-At-A-Time SA
Assumption: Factors are linearly independent (no interactions).
Benefits: Easy to implement and interpret.
Limits: Ignores potential interactions.
All-At-A-Time SA
Number of different sampling strategies: full factorial, Latin hypercubes, more.
Benefits: Can capture interactions between factors.
Challenges: Can be computationally expensive, does not reveal where key sensitivities occur.
Local SA
Local sensitivities: Pointwise perturbations from some baseline point.
Challenge: Which point to use?

Global SA
Global sensitivities: Sample throughout the space.
Challenge: How to measure global sensitivity to a particular output?
Advantage: Can estimate interactions between parameters

How To Calculate Sensitivities?
Number of approaches. Some examples:
- Derivative-based or Elementary Effect (Method of Morris)
- Regression
- Variance Decomposition or ANOVA (Sobol Method)
- Density-based (\(\delta\) Moment-Independent Method)
Example: Lake Problem
Parameter Ranges
For a fixed release strategy, look at how different parameters influence reliability.
Take \(a_t=0.03\), and look at the following parameters within ranges:
| Parameter | Range |
|---|---|
| \(q\) | \((2, 3)\) |
| \(b\) | \((0.3, 0.5)\) |
| \(ymean\) | \((\log(0.01), \log(0.07))\) |
| \(ystd\) | \((0.01, 0.25)\) |
Method of Morris
The Method of Morris is an elementary effects method.
This is a global, one-at-a-time method which averages effects of perturbations at different values \(\bar{x}_i\):
\[S_i = \frac{1}{r} \sum_{j=1}^r \frac{f(\bar{x}^j_1, \ldots, \bar{x}^j_i + \Delta_i, \bar{x}^j_n) - f(\bar{x}^j_1, \ldots, \bar{x}^j_i, \ldots, \bar{x}^j_n)}{\Delta_i}\]
where \(\Delta_i\) is the step size.
Method of Morris
Sobol’ Method
The Sobol method is a variance decomposition method, which attributes the variance of the output into contributions from individual parameters or interactions between parameters.
\[S_i^1 = \frac{Var_{x_i}\left[E_{x_{\sim i}}(x_i)\right]}{Var(y)}\]
\[S_{i,j}^2 = \frac{Var_{x_{i,j}}\left[E_{x_{\sim i,j}}(x_i, x_j)\right]}{Var(y)}\]
Sobol’ Method: First and Total Order
┌ Warning: The `generate_design_matrices(n, d, sampler, R = NoRand(), num_mats)` method does not produces true and independent QMC matrices, see [this doc warning](https://docs.sciml.ai/QuasiMonteCarlo/stable/design_matrix/) for more context. │ Prefer using randomization methods such as `R = Shift()`, `R = MatousekScrambling()`, etc., see [documentation](https://docs.sciml.ai/QuasiMonteCarlo/stable/randomization/) └ @ QuasiMonteCarlo ~/.julia/packages/QuasiMonteCarlo/KvLfb/src/RandomizedQuasiMonteCarlo/iterators.jl:255
Sobol’ Method: Second Order
Example: Cumulative CO2 Emissions

Model for CO2 Emissions
Example: Cumulative CO2 Emissions
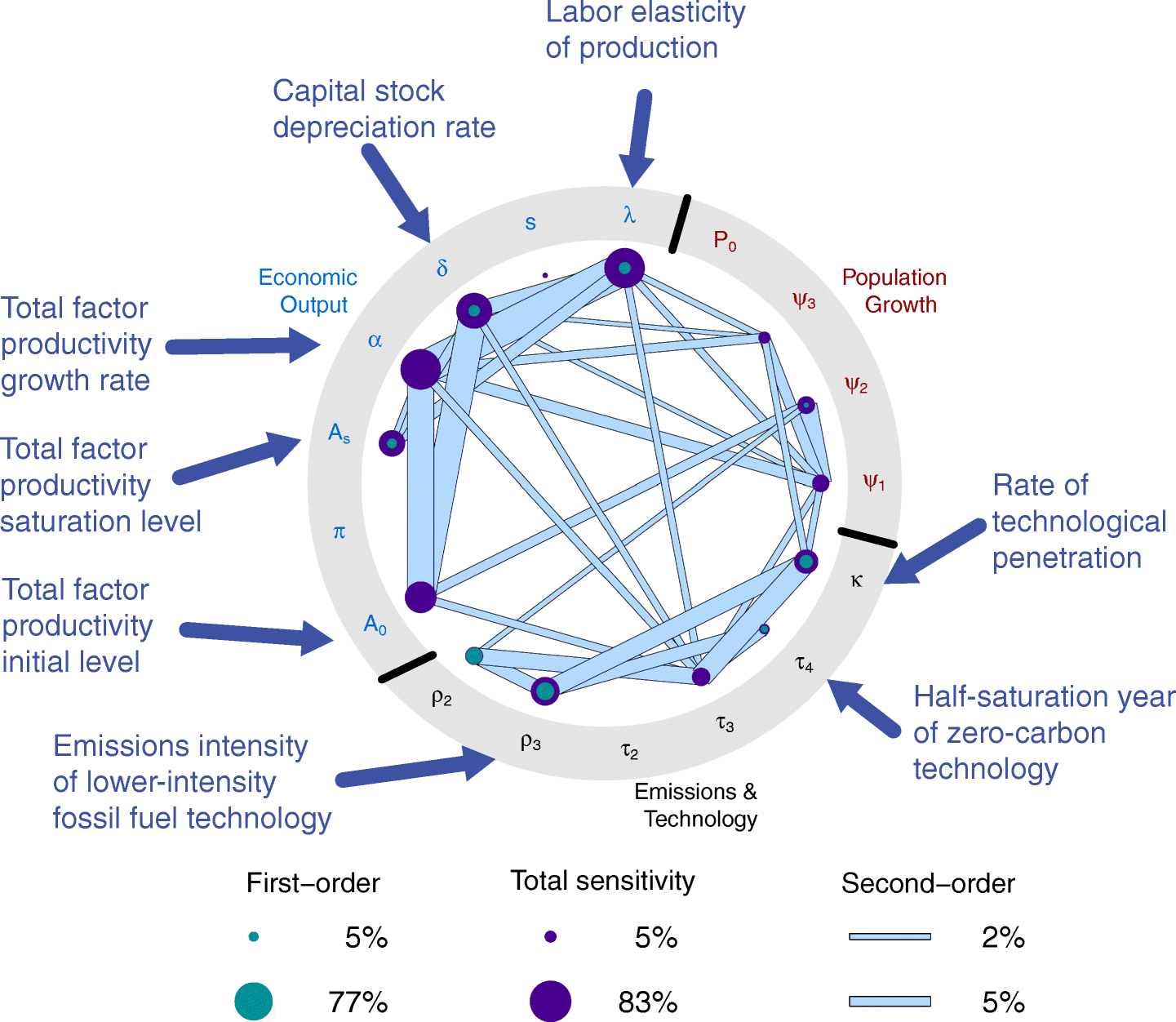
CO2 Emissions Sensitivities
Source: Srikrishnan et al (2022)
Key Takeaways
Key Takeaways
- Sensitivity Analysis involves attributing variability in outputs to input factors.
- Factor prioritization, factor fixing, factor mapping are key modes.
- Different types of sensitivity analysis: choose carefully based on goals, computational expense, input-output assumptions.
- Many resources for more details.
Upcoming Schedule
Next Classes
Monday: Multiple Objectives and Tradeoffs
Assessments
Today: Lab 4 Due