Dissolved Oxygen
Lecture 07
September 8, 2023
Review and Questions
Last Class
- Model-based simulation as a way to understand system dynamics and response.
- Box models: mass-balance in some region of the domain
- Can generalize single box models by:
- Adding more complexity;
- combining multiple boxes.
Why Simulate?
- System involves complex, nonlinear dynamics that may not be analytically tractable.
- Setting up and running a real-world experiment is not possible.
- State depends on prior states or states of nearby locations, so need to iterate over multiple spatial or temporal steps.
- Need to understand range of system performance across rarely-seen conditions.
Questions

Text: VSRIKRISH to 22333
Dissolved Oxygen Overview
Fate & Transport Modeling
How do nutrients and other quantities move through environmental mediums?
What can make fate & transport modeling more complex?
- Multiple points of inflow;
- More complex growth/decay dynamics.
- Stochasticity/randomness.
Dissolved Oxygen
Dissolved oxygen (DO) is the free, non-compound oxygen present in water or other liquids.
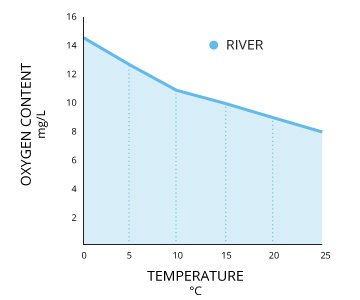
Freshwater can only hold small amounts, and this capacity is regulated by temperature.
Source: fondriest.com
Temperature Impact on DO

Dissolved Oxygen and Temperature Plot
Source: usgs.gov
Dissolved Oxygen and Life
Dissolved oxygen is an important nutrient for aquatic life.
Hypoxia occurs when DO levels are \(< 2\) mg/L.

Source: fondriest.com
Factors Influencing DO
- Temperature, Pressure, Depth
- Salinity
- Mixing
- Plant and Microbial Life
- Organic Matter
Impact of Paris On Seine DO, 1874

Dissolved Oxygen Downstream of Paris, 1874
Source: Dmitrieva, T., et al. (2018). https://doi.org/10.1007/s12685-018-0216-7
DO Regulatory Standards
Objective: Keep DO above the regulatory standard.
In NY (via Westlaw):
- DO levels may not fall below 3 mg/L
- DO may not be below 4.8 mg/L for an extended period
Modeling Dissolved Oxygen
Oxygen Balance in Rivers and Streams
Selecting a Metric for DO Fluxes
Typically use oxygen demand (OD):
- measure of the concentration of oxidizable materials in a water sample
- metric for organic waste contamination
- reflects how oxygen will be depleted in a given segment
But there are several different processes affecting total OD!
Biochemical Oxygen Demand (BOD)
Oxygen used by microbes during aerobic decomposition of organic materials: \[\text{Organic Matter} + \text{O}_2 \rightarrow \text{CO}_2 + \text{H}_2\text{O} + \text{NO}_3 + \text{SO}_2 + \text{Residuals}\]
Broadly speaking, we care about two types of BOD: Carbonaceous BOD and Nitrogenous BOD.
Carbonaceous BOD (CBOD)
Oxygen consumed during microbial decomposition of carbon compounds, e.g.: \[\text{C}_a\text{H}_b\text{O}_c + d\text{O}_2 \rightarrow e\text{H}_2\text{O} + f\text{CO}_2\]
Nitrogenous BOD (NBOD)
Oxygen consumed during microbial decomposition of nitrogen compounds: \[2\text{NH}_2^+ + 4\text{O}_2 \rightarrow 2\text{H}_2\text{O} + 4\text{H}^+ + 2\text{NO}_3^-\]
BOD and Time
Moreover, BOD is differentiated based on time frame, e.g.:
- BOD5: oxygen demand over 5 days
- BOD20: oxygen demand over 20 days
DO Modeling Needs
Need a model that will predict DO as a function of CBOD, NBOD.
Use a fate and transport modeling approach: how are relevant quantities moved downstream?
Note: Can’t assume homogeneous processes.
Modeling DO
So what do we do?
Start by assuming steady-state waste in each section (or box…).
Modeling DO
We’ll track the mass balance in terms of rates (not absolute mass).
What happens to an element of water?
Steady-State Waste, DO Mass Balance
Let \(U\) be the river velocity (km/d), \(x\) the distance downstream from a waste release site in km, and \(C(x)\) the DO concentration at \(x\) in mg/L.
\[\begin{align} U \frac{dC}{dx} &= \text{Change in DO} \\[0.5em] &= \text{Reaeration} + \text{Photosynthesis} - \text{Respiration} \\[0.5em] & \qquad - \text{Benthal Uptake} - \text{CBOD} - \text{NBOD} \end{align}\]
BOD Oxygen Uptake
Assume deoxygenation from waste decomposition is first-order (rate \(k\)):
\[\begin{aligned} \frac{dM}{dt} &= -kM \\\\ \Rightarrow M &= M_0 \exp(-kt) \end{aligned}\]
But our equations are formulated in terms of distance:
\[M = M_0 \exp(-kx/U)\]
BOD Oxygen Uptake
For biochemical organics, if \(k_c\) is the deoxygenation rate (d\(^{-1}\));
\[B(x) = B_0 \exp(-k_c x / U);\]
For nitrification, if \(k_n\) is the deoxygenation rate (d\(^{-1}\)):
\[N(x) = N_0 \exp(-k_n x / U).\]
Steady-State Waste, DO Mass Balance
So the corresponding oxygen uptake rates are \[k_c B(x) = k_c B_0 \exp(-k_c x / U)\] and
\[k_n N(x) = k_n N_0 \exp(-k_n x / U).\]
Steady-State Waste, DO Mass Balance
Other processes:
Reaeration, assume a simple linear model based on difference from saturation level \(C_s\): \(k_a (C_s - C)\)
Assume measured, constant values for photosynthesis (\(P_s\)), respiration (\(R\)), benthal uptake (\(S_B\))
Steady-State Waste, DO Mass Balance
Putting it all together:
\[\begin{aligned} U \frac{dC}{dx} &= k_a (C_s - C) + P - R - S_B \\\\ &\quad - k_cB_0\exp\left(\frac{-k_cx}{U}\right) - k_n N_0\exp\left(\frac{-k_nx}{U}\right) \end{aligned}\]
Key Points
Key Points
- Dissolved oxygen (DO) is essential for water quality and aquatic life.
- Commonly regulated to keep DO above a minimum threshold.
- DO impacted by a number of factors, notably organic waste decomposition and nitrification.
- We derived a first-order equation for DO using mass-balance and fate & transport principles.
Upcoming Schedule
Next Classes
Monday: Simulating DO dynamics.
Wednesday/Friday: Uncertainty and Risk
Assessments
- HW1 due tonight (9PM!)